Constraint satisfaction and the colouring problem

What is Constraint Satisfaction Problem?

A Constraint Satisfaction Problem (CSP) consists of:

• a set of variables $\mathcal{X} = \{x_1,…,x_n\}$,
• a set containing the domains of each variable $\mathcal{D} = \{D_x \mid \forall_x \in \mathcal{X}\}$,
• and a set of constraints restricting the values that the variables can simultaneously take $\mathcal{C} = \{C_1, C_2, …, C_n\}$.

Note that values need not be a set of consecutive integers (although often they are). They need not even be numeric.

A solution $M$ to a CSP is an assignment of a value from its domain to every variable, in such a way that every constraint is satisfied. We may want to find:

• just one solution, with no preference as to which one,
• all solutions,
• an optimal, or at least a good solution, given some objective function defined in terms of some or all of the variables; in this case we speak about Constraint Optimisation Problem (COP)

Colouring Australia States

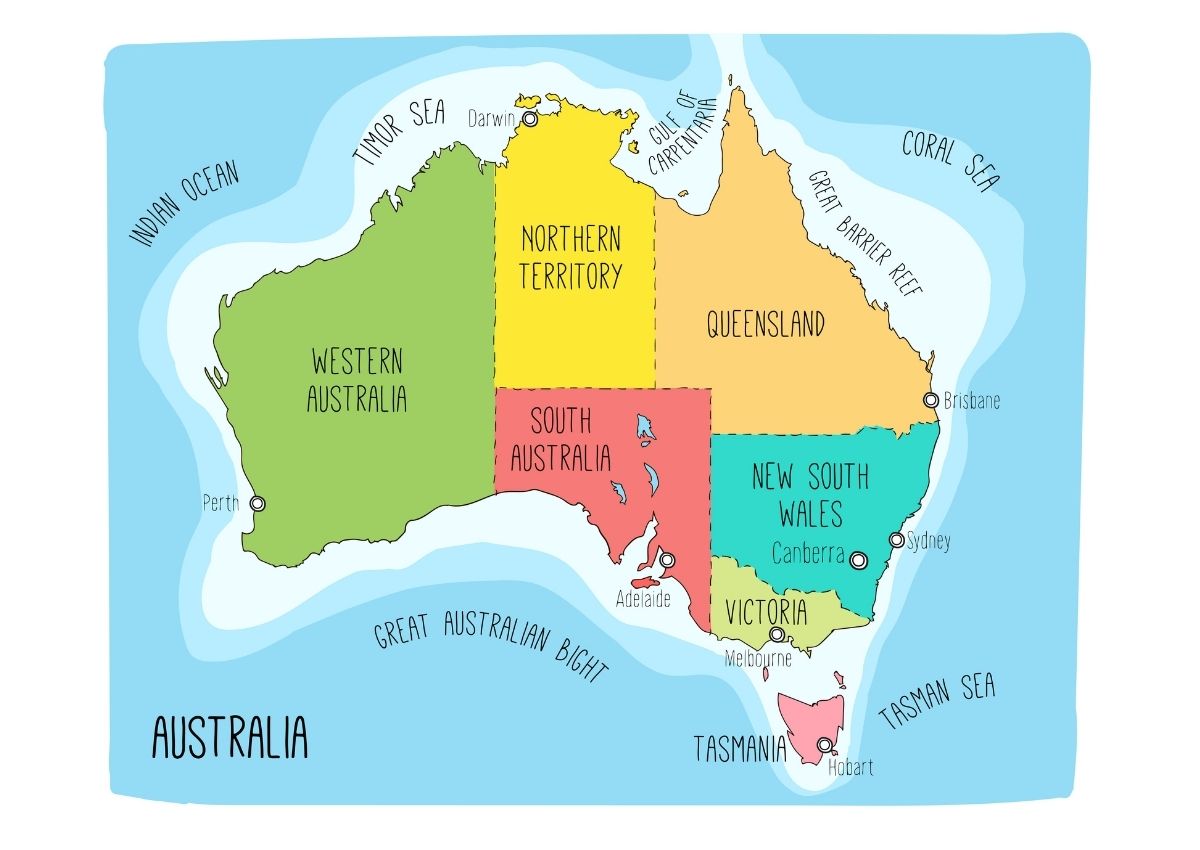
Imagine that we wish to colour a map of Australia as shown in the next figure. It is made up of seven different states and territories each of which must be given a colour so that adjacent regions have different colours.

Note that this problems is simpler than ask for the minimal number of colors that we need to use to colour the map. Such problem is named chromatic number of a graph.

We can represent the map of Australia as a graph, where each node or vertex is a region and each arc or edge represent whenever a given region is adjacent to another region.

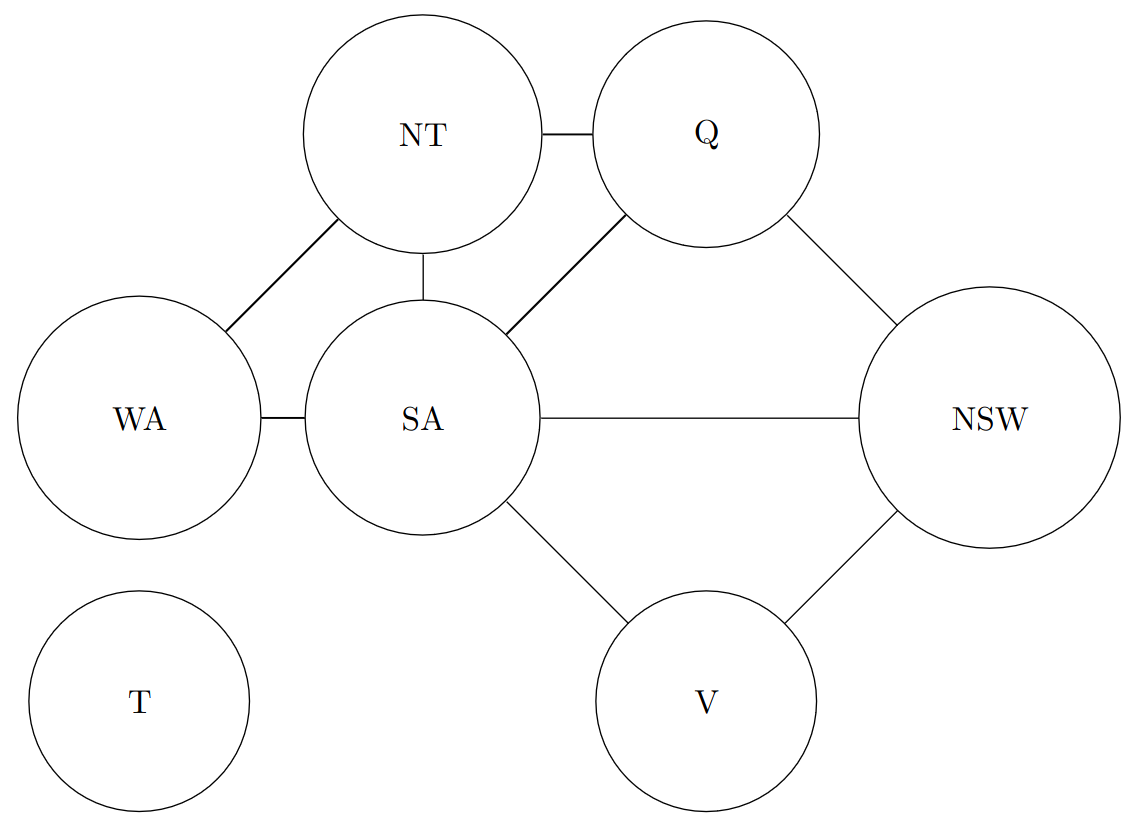
Map of Australia represented as a graph

Now, lets model this problem as a CSP problem. For that we need to define $\mathcal{X, D} \ \text{and} \ \mathcal{C}$ aswell as the type of solution we want $M$.

• As the requirements ask to find a possible solution for the colour problem, we want to find just one solution, with no preference as to which one, i.e., $M = \text{satisfy}$,
• the variables are the regions of Australia, hence $\mathcal{X} = \{WA, NT, Q, NSW, SA, V, T\}$,
• the domain of each variable is not defined, but lets say that we do not want to use more than 3 colours to colour the map of Australia $\{\{1..3\}_x \mid \forall_x \in \mathcal{X}\}$,
• and finally the constraints, they are simple as we do not want to colour adjacent regions with the same colour, hence the constraints $\mathcal{C}$ are the following:

\[\begin{eqnarray} WA \neq NT \\ WA \neq SA \\ NT \neq SA \\ NT \neq Q \\ Q \neq NSW \\ SA \neq Q \\ SA \neq NSW \\ SA \neq V \\ NSW \neq V \end{eqnarray}\]

MiniZinc to Model the Colouring Problem

MiniZinc is a high-level constraint modelling language that allows you to easily express and solve discrete optimisation problems. As any other language it has its own syntax and concepts that we need to learn, e.g., keywords, decition variable, constant, etc.

int: nc = 3;

var 1..nc: wa;   var 1..nc: nt;  var 1..nc: sa;   var 1..nc: q;
var 1..nc: nsw;  var 1..nc: v;   var 1..nc: t;

constraint wa != nt;
constraint wa != sa;
constraint nt != sa;
constraint nt != q;
constraint sa != q;
constraint sa != nsw;
constraint sa != v;
constraint q != nsw;
constraint nsw != v;

solve satisfy;

output ["wa=\(wa)\t nt=\(nt)\t sa=\(sa)\n",
        "q=\(q)\t nsw=\(nsw)\t v=\(v)\n",
         "t=", show(t),  "\n"];

If we save the code above in a file call aust.mzn and we execute it, we may expect a result as the following:

$ minizinc aust.mzn

wa=3	 nt=2	 sa=1
q=3	 nsw=2	 v=3
t=1
----------