Introduction to Programming in C++
Check out the original notebook here.
Table of content
- Definitions
- Template for programs
- Built in types
- The typedef keyword
- Code examples
Definitions
Before digging into code examples and programs written in C++ we need to define what an algorithm, a programming language and a computer program are.
Algorithm
An algorithm is a method or function for solving a problem. From the imperative point of view, an algorithm is usually described as a sequence of steps. But other paradigms such as the functional one defines an algorithm as a composition of pure functions that operates on inmutable data without side-effects.
In this course we will use the first definition, as we are working with C++ with is a clearly imperative programming language.
Programming language
A programming language is a language used to describe a program that must be understood by a computer.
A programming langue has:
- Data (numbers, strings, complex-structures, …)
- Instructions (arithmetic, sequence, repetition, …)
A programming languge has its own syntax and semantics, depending on the programming language it is very strict or no, but it must be understood by a computer.
Computer Program
A computer program is an algorithm written in a programming language to solve a problem.
What kind of algorithm can be written? For instance:
- Calculate the square root of a number
- Play a music file
- Find the shortest path between two cities
- $\cdots$
Yet not all poblems have an algorithm to solve them. And not all algorithms have the same complexity nor problems are of the same complexity class.
Template for programs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#ifdef _WIN32
#include <windows.h>
#endif
using namespace std;
/***** algorithm *****/
int main() {
#ifdef _WIN32
SetConsoleOutputCP( 1252 );
SetConsoleCP( 1252 );
#endif
cout << "Hola company!" << endl;
cout << "Amb la teva col·laboració i força assolirem el cim!" << endl;
return 0;
}
For every deliverable programs I recommend you to use the above template. Why? Because it has already has boiled code that ensures code to run in the most common work statations, aka, Windows.
Let’s brake it in different sections to understand what it does:
1
2
3
#ifdef _WIN32
#include <windows.h>
#endif
This piece of code is only taken into account if a C++ compiler for Windows is detected. If a C++ compiler for Windows is detected it includes the library windows.h which defines a very large number of Windows specific functions that can be used in C or C++.
1
2
3
4
#ifdef _WIN32
SetConsoleOutputCP( 1252 );
SetConsoleCP( 1252 );
#endif
This other piece of code is executed when the main functions is executed. It checks again if a C++ compiler for Windows is deteced, if so, defines the codification type for input and output of the Window console. What it does in reallity is to add support for some latin characters, i.e., words with accents and other latin codification to represent charts.
1
main();
Hola company!
Amb la teva col·laboració i força assolirem el cim!
Built in types
In this section we will talk about the basic types that C++ language provides built-in.
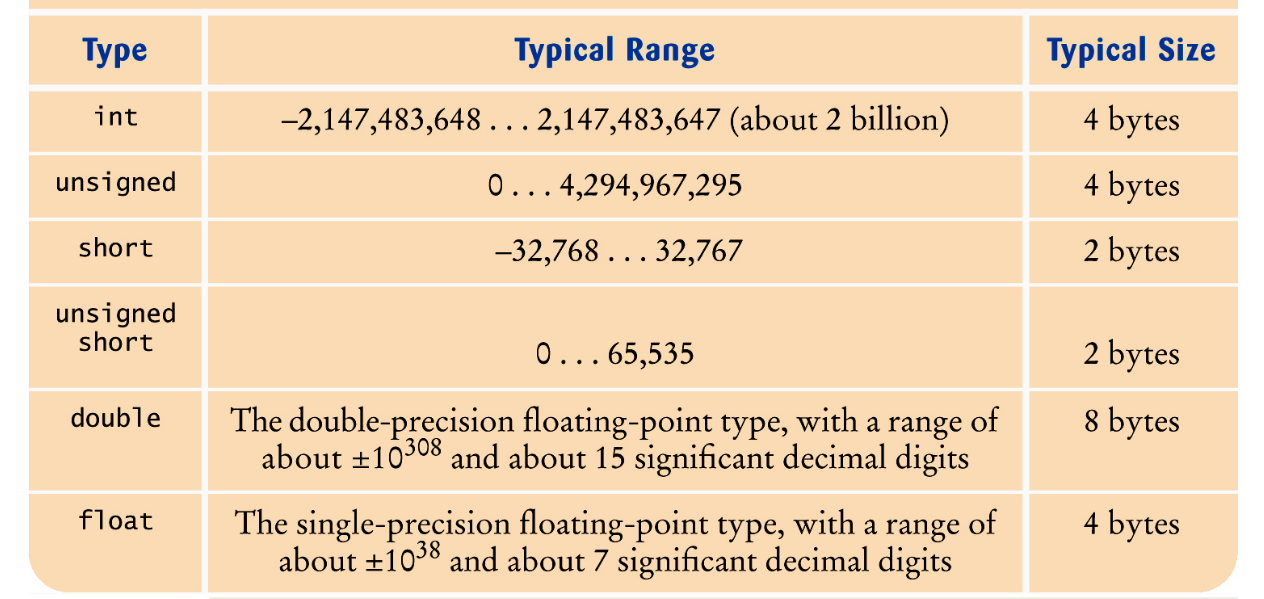
Numeric types
Let’s start with numeric types (see image below). There are many types of numbers, numeric types have a determined limit range. When the range is over-passed we call it overflow. Compiler won’t tell you when an error of this kind exist, so be careful!. If it happends, the result of the operation is truncated and it gives a value between the range of the type.
Char type
The char keyword is used to declare character type variables. A character variable can store only a single character. Notice that character must be sorrounded by ' which is the single quotation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
char fst_vowel = 'a';
char lst_vowel = 'u';
char fst_digit = '1';
char lst_digit = '9';
std::cout << "Vowels..." << std::endl;
std::cout << fst_vowel << std::endl;
std::cout << lst_vowel << std::endl;
std::cout << std::endl;
std::cout << "Digits..." << std::endl;
std::cout << fst_digit << std::endl;
std::cout << lst_digit << std::endl;
Vowels...
a
u
Digits...
1
9
String type
Well before I explain how to work with string you must now that there is the concept of namespace. A namespace is an environment from which you use types, keywords, functions, etc. Most of the times, when you use code of third parties or libraries you would prefer to refer it by the specfic namespace because to avoid naming conflicts.
In this case, we can import all the code from the standard library instead of using it intentionaly the the use of :: as follows:
1
using namespace std;
1
2
3
4
5
6
7
8
9
#include <iostream>
using namespace std;
string hola = "hola";
string holax2 = hola + hola;
cout << hola << endl;
cout << holax2 << endl;
hola
holahola
The typedef keyword
The keyword typedef is a reserved C++ keyword and it allows to rename an existing type. Most of the times you would use this keyword to give meaning at your code and documentation.
1
2
3
4
5
6
#include <iostream>
#include <string>
using namespace std;
typedef string Day;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int main() {
Day monday = "monday";
Day tuesday = "tuesday";
Day wednesday = "wednesday";
Day thuesday = "thuesday";
Day friday = "friday";
Day saturday = "saturday";
Day sunday = "sunday";
cout << monday << endl;
cout << tuesday << endl;
cout << wednesday << endl;
cout << thuesday << endl;
cout << friday << endl;
cout << saturday << endl;
cout << sunday << endl;
return 0;
}
1
main();
monday
tuesday
wednesday
thuesday
friday
saturday
sunday
Code examples
Sum of 2 natural numbers
Let’s create a program that reads two natural numbers and prints the sum.
1
2
3
4
5
6
7
8
9
10
#include <iostream>
int main() {
int x, y;
std::cin >> x >> y;
int s = x + y;
std::cout << s << std::endl;
return 0;
}
1
main();
2
2
4
Notice that we use the commands cin to read from the standard input (keyboard) and cout to print values in the standard output (screen).
Sometimes it is usuful to document our programs, we do it by the use of comments.
- Comments are use to give context to other programmers (although you can do it by structuring and namming correctly)
- Compilers ignore the comments
In C++ comments are made by the use of:
// <text>: comments the text that follows it till the end of the line/* <text> */: comments the block of text inside it and it may content multiple lines
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
/*
This program reads two natural numbers
and shows the sum of them
*/
int main() {
// declares two variables of type int
int x, y;
/*
reads from standard input and assign
to each variable the corresponding value read
*/
std::cin >> x >> y;
// declares and initializes a new variable
int s = x + y;
// prints the value of the initialized variable
std::cout << s << std::endl;
return 0;
}
1
main();
4
5
9
Calculate $x^y$
Computing the potence of $x^y$ means multipling $x$ a total of $y$ times:
\[\underbrace{x \times x \times x \times \dots x}_{y \text{\ times}}\]To do things easely lets define $x \in \mathbb{R}$ and $y \in \mathbb{N}$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <iostream>
int main() {
int x, y;
std::cin >> x >> y;
int i = 0;
int p = 1;
while (i < y) {
i = i + 1;
p = p * x;
}
std::cout << p << std::endl;
}
1
main();
10
3
1000
Prime factors
Let’s create an algorithm that decompose numers into its prime factors. For instance, the prime numbers of number $350$ are ${2, 5, 5, 7}$.
Algorithm description:
- Try all potential divisiors of number $n$ starting from the divisor $d = 2$
- If the number $n$ is divisible by $d$, divide $n$ by $d$ and try again the same divisor $d$ against the result
- If not divisible, go to the next divisor
- Keep dividing until the number $n$ becomes $1$
Notice that $n$ and $d$ $\in \mathbb{N}$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <iostream>
int main() {
int n;
int d = 2;
std::cin >> n;
while (n != 1) {
if (n % d == 0) {
// d is a divisor of n
std::cout << d << " ";
n = n / d;
}
else {
// d is not divisor of n, so we try a new divisor
d = d + 1;
}
}
return 0;
}
1
main();
350
2 5 5 7
QUESTION: This algorithm only yields prime factors (an not non-prime factors). Why?
Answer:
The algorithm starts with $d = 2$, the smallest prime number. If $n$ is divisible by $d$, $d$ is a factor and is printed. After dividing $n$ by $d$, the algorithm continues with the new value of $n$.
The key point is that once all factors of $d = 2$ are extracted, $d$ is incremented to $3$, then $4$, and so on. If $d$ is a composite number (e.g., 4), by the time the algorithm reaches $d$, all smaller prime factors (e.g., 2) have already been extracted from $n$.
Therefore, $n$ is no longer divisible by composite numbers like 4, 6, 8, etc., because those would have been divisible by smaller primes that were already factored out.